「ABC予想」の次は「リーマン予想」だ！

2020/4/28

リーマン予想の今,そして解決への展望

　数学の超難問「ABC予想」を証明したとされる論文が、ついに国際的な数学誌に掲載されることになり、数学への関心が高まっている。

　それにしても、未解決難問の中でも飛びぬけて難しいと言われている「リーマン予想」の研究がここまで進んでいるとは、関係者以外のだれが想像できただろうか。それも共同研究といった様相である。

19世紀から持ち越された

　本書『リーマン予想の今,そして解決への展望』（技術評論社）の著者・黒川信重さんは、1952年生まれの東京工大名誉教授。リーマン予想研究をけん引する１人でもある。同予想研究に関連する新しい手法「絶対数学」の提唱者として世界に知られる存在だ。

　本書は、同予想の発端から研究の主な到達点を概説し、新しいアプローチを紹介する。

　リーマン予想は1859年にB・リーマンが提唱した。1900年に当時の数学界のリーダーだったヒルベルトが、数学の最重要な23の未解決問題の一つにリストアップ。その後１世紀が過ぎても、持ち越され、2000年に発表された「ミレニアム問題」にも挙げられている。

　未解決問題は「フェルマーの最終定理」や「ポアンカレ予想」が解かれてしまったが、数多く残されている。リーマン予想はとりわけ難攻不落だとされる。

　この予想はどんなものなのか。簡単に押さえておこう。

　ゼータ関数「ζ（s）」の性質についての予想だ。こんな式になる。

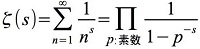
　整数と素数の関係を表す。これにはオイラーに始まる歴史がある。

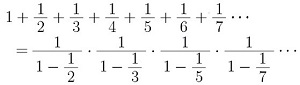
　ゼータ関数で言えばs＝1に当たる。左辺に全自然数の逆数の総和、右辺はすべての素数が登場する多項式の無限積だ。オイラー積と呼ばれる。全自然数の和が、全素数の式に初めて因数分解された。整数と素数の関係である。このsを複素数と素数の関係にまで拡張したのが後のリーマンだった。

　ゼータ関数はsの取り方によって値が0になる。これをゼロ点と呼ぶが、そのときの「ｓの実部と虚部のうち、実部はすべて1/2（sが負の整数の場合、0になるのは自明なので除く）」というのがリーマン予想の主張だ。

研究史の発展が辿れる

　この予想の解明には、さまざまなアプローチが試みられてきた。黒川さんが特に重要だとして紹介するのは次の通りだ。

　・オイラー積とラマヌジャン
　・有限体
　・合同ゼータ関数
　・深リーマン予想
　・一元体、絶対数学
　・零和構造と黒川テンソル積

　概ね古い順に解説されていて、数学者が研究をどのように発展させてきたかを辿れるようになっている。ただ、内容を正確に理解するのは難しく、数学科でも数論以外の専攻者には敷居が高いものだ。

　それでも本書の内容をごく簡単にまとめておこう。オイラー積ζ（s）の研究はsの拡張の歴史だった。リーマンは複素数に拡大、ラマヌジャンはsを指数に広げた。

　さらにsを関数にする試みも行われた。Sの関数化というのは、変数sのほかにXやYを加えてゆくやり方だ。多重化と呼ばれる。合同ゼータ関数や黒川テンソル積はこの流れに位置する。

　では、多重化とはどんなものなのか。例えば関数f（ｘ）＝αxに1つ変数を加えてf（ｘ,y）＝αx＋βyにする。元の関数とは別物になるが、yを固定すると、f（ｘ,y）は一定の歪みを持ちながら元のf（ｘ）が再現されるという特徴を持っている。つまり、ゼータ関数ζ（s）で言うと、ζ（s,w）ではwが固定されると、ζ（s）が再現されるということになる。ζ（s）を研究するのに、なぜこんな回りくどいことをするのかと疑問に思うかもしれないが、理由はちゃんとある。多重化した方が、リーマン予想を解決しやすいからだ。wを加えて多重化した関数では既に、実部がすべて1/2になることが証明されているのだそうだ。

　このほか、有望なアプローチとして「零和構造」にも言及している。ζ（α,X）＝0かつζ（β,Y）＝0ならば、ζ（α+β、X+Y）も0になる――というものだ。

手法を公開、参戦を呼びかける

　数学研究は解くための手法を思いついた研究者が密かに進めるのが常だ。フェルマーの最終定理を解いたA・ワイルズ（1995年）や、ポアンカレ予想のG・ペレルマン（2002年）が孤独のうちに解決したことは記憶に新しい。

　しかし黒川さんは、プロフィールで紹介した絶対数学の着想以降、早々とこの手法を公開、広く参戦を呼びかけている。フランスのフィールズ賞数学者アラン・コンヌらもその可能性を評価し、参戦している。本書も、黒川さんのオープンな気風の表れで、読むことがあれば、きっとすがすがしい気分になるだろう。

　余談になるが、オープンな研究と言えば、同じ数論のP・エルデシュがいる。定住せず研究者宅を訪れては共同研究をするので、「放浪の数学者」と呼ばれる。エルデシュの名に因んで命名された「数」がある。「エルデシュ数」だ。彼との共著論文を持つ学者は「1」、その共著者と共著のある研究者は「2」となる。エルデシュとの隔たりを表す数だ。例えば評者なら、このエルデシュ数は無限大だ。

　もしも同様に「リーマン数」があれば、黒川さんのこの数はきっと1桁になるに違いない。本書は、リーマン数が持てるかどうかの人や、これから数論の世界に入るかどうかに迷っている若者に、展望を提供するはずだ。

　黒川さんには『リーマンと数論』（共立出版）、『リーマン予想を解こう新ゼータと因数分解からのアプローチ』（技術評論社）、『ラマヌジャン探検――天才数学者の奇蹟をめぐる』(岩波科学ライブラリー)、『絶対ゼータ関数論』（岩波書店）、『絶対数学』（日本評論社、共著）、『ガロア理論と表現論　ゼータ関数への出発』（日本評論社）など多数。

（BOOKウォッチ編集部　森永流）